UNIDAD 3: Limites y continuidad.

Cañedo Huerta Juan Isaias             No. control: 15260694

3.1. Limite de una sucesión.

La definición del limite de una sucesión significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.

Matemáticamente la definición puede ser demostrada suponiendo an} sea la sucesión y l un número real. Si por cada ε › 0 entonces encontramos m N, tal que , n N, es l y se escribe an=l. Esto se lee como: Como n tiende al infinito, tiende a l.

Ademas, si para una sucesión an se podemos encontrar un numero M positivo, tal que, | an | M n N entonces la sucesión { an } se dice que es cerrada.

Similarmente, las sucesiones pueden estar creciendo o decreciendo.

Algunas de las propiedades generales de los Límites de una Sucesión incluyen:

1).Los Límites de las sucesiones de origen convergentes son únicos.

2). Una sucesión de origen convergente es siempre cerrada y viceversa.


En palabras mas sencillas el límite de una sucesión es el número al cual se van aproximando los términos de una sucesión.

3.2 Limite de un función de variable real.

Se llama función real de variable real a toda aplicación f de un subconjunto no vacío S de R en R

Una función real está definida, en general, por una ley o criterio que se puede expresar por una fórmula matemática. La variable x recibe el nombre de variable independiente y la y o f(x) variable dependiente o imagen.

Considérese la función definida por: y= f(x) = 2x²-x-1/x-1 ; x 1 el único punto en el cual f(x) no está definida es en x = 1, pero, en puntos tan cercanos a 1 como se quiera, la función se encuentra definida. Esta situación da lugar a la siguiente pregunta: ¿Se aproxima f(x) a algún valor específico, cuando x se aproxima a 1?

Cuando x se aproxima a 1 por la izquierda (valores menores que 1) y por la derecha de 1 (valores mayores que 1).

a medida que los valores de x, se “acercan” a 1, sin tomar el valor de 1, los valores de f(x) se “acercan” a 3. Dándole a la palabra límite un significado intuitivo, se dice que:

El “límite” de la función f(x) es 3 cuando x tiende a 1. La afirmación anterior frecuentemente se expresa simbólicamente por cualquiera de las formas:

F (x) =3 cuando x–>1 (se lee: f(x) tiende a 3 cuando x tiende a 1).

Ejercicios resueltos de limite de una funcione de variable real

3.3 Calculo de limites.

Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:

Es decir: Para calcular el límite se sustituye en la función el valor al que tienden las x.

No podemos calcular  porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.

Ejemplos:

3.4 Propiedades de los limites.

Los límites forman una parte fundamental del cálculo en las Matemáticas. De hecho, el primer punto en el concepto del cálculo está marcado por los límites. Los límites pueden ser entendidos fácilmente al observar sus propiedades.

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.

Estas son las propiedades mas importantes de los limites:

3.5 Limites laterales.

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x - a^- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.

• x - a⁺ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.

Nota.- Una función tiene límite si los límites laterales son iguales, es decir, cuando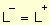

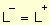
En algunas funciones como las definidas por partes y las de dominio restringido, como las que tienen raíces cuadradas, se aplican los límites laterales.

El límite lateral por la derecha de una función y = f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores mayores que a .

El límite lateral por la izquierda de una función y=f(x) en el punto x = a es el valor al que se aproxima f(x) cuando x se aproxima al valor de a por valores menores que a .

Ejemplo:

Indicar si la siguiente funcione tiene límites en los puntos indicados:

3.6 Limites infinitos y limites al infinito.

El símbolo 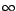 se lee infinito, es de carácter posicional, no representa ningún número real. 

Si una variable independiente 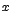 está creciendo indefinidamente a través de valores positivos, se escribe  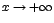(que se lee:  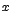tiende a más infinito), y si decrece a través de valores negativos, se denota como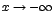(que se lee:  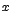tiende a menos infinito). 

Similarmente, cuando 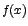 crece indefinidamente y toma valores positivos cada vez mayores, se escribe 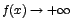, y si decrece tomando valores negativos escribimos . 

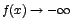Limites infinitos

Decimos que lim f(x)= si para los valores de x proximos a a,     x→ a    los valores de f(x) pueden hacerse tan grandes como queramos.

Con rigor, decimos que lim f(x)= si fijado a un valor k positivo y tan grande como se quisiera, existe un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entoces f(x)>k.

Análogamente,    lim f(x) = – 

x→a 

si para los valores de x cercanos a a, los valores de f(x) se pueden hacer tan pequeños como queramos.

Diremos que lim f(x) = – 

x→a 

si fijado un valor de k positivo y tan grande como se quisiera, podemos encontrar un entorno de a, E(a, ∂), tal que si x ∈ E (a,∂ ) y x ≠ a, entonces  f(x) < -k

Limites al infinito

Cuando el dominio de y= f(x) se extiende indefinidamente hacia la derecha o hacia la izquierda de la recta real tienen sentido las expresiones:

• lim f(x) = L si “haciendo x arbitrariamente grande”, los valores de f(x) se acercan a L.

x→ 

•lim f(x) = L si “haciendo x arbitrariamente pequeña, los valores de f(x) se acercan a L.

         x→

Ejemplo:

3.7 Asíntotas

Las asíntotas son rectas a las cuales la función se va acercando indefinidamente.

La asíntota de una función particular es una recta tal que la distancia entre el gráfico de la función y la recta de la asíntota se aproximan a 0 a medida que estos avanzan hacia el infinito. En otras palabras, se dice que una recta es asíntota para una curva D con la condición que el límite de la distancia del punto Q sobre la curva al punto de la recta de la asíntota es 0. Las asíntotas son curvas cuya apariencia es específicamente y = f (x).

Las asíntotas de una función siguen una importante propiedad que establece que la alteración de una función contiene una asíntota solo si la función correspondiente original tiene una asíntota.

Las Asíntotas se pueden clasificar en tres tipos; asíntota vertical, asíntota horizontal y asíntota oblicua.


La aparición de asíntotas horizontales puede encontrarse en su mayoría en funciones fraccionarias, en las cuales, el numerador se acerca a un determinado valor positivo o negativo, mientras el denominador se mueve hacia el infinito.


Las Asíntotas Verticales son las rectas verticales hacia las cuales se mueve el gráfico de una función determinada. Estos tipos de asíntotas ocurren cuando el denominador se aproxima a 0, mientras que el numerador no lo hace.


Las asíntotas oblicuas son las rectas no paralelas al eje x o al eje y. Debido a su apariencia inclinada, también se les conoce como asíntotas inclinadas.

Ejemplo:

3.8 Funciones continuas y discontinuas en un punto y en un intervalo.

Una función continua es aquella que responde a las variaciones de cada minuto en la entrada de la función por lo que muestra variación en la salida de la función.

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:

1. Que el punto x= a tenga imagen.

2. Que exista el límite de la función en el punto x = a.

3. Que la imagen del punto coincida con el límite de la función en el punto.

Si una función no es continua en un punto x=a, diremos que es discontinua en dicho punto.

Una función puede ser discontinua en un punto o para un intervalo completo.

Una función que es discontinua en un punto debe cumplir dos requisitos:

• Tanto del lado izquierdo así como del derecho debe existir un límite para la función en el punto dado.

• Ambos límites deben ser finitos naturales.

Si la discontinuidad puede ser eliminada entonces es de primer orden, mientras que si no puede ser eliminada se conoce como discontinuidad de segundo orden.

Ejemplos:

Ej. 1: Demostrar que f(x) = 5 es continua en 7.

Solución: debemos verificar que las tres condiciones se cumplan.

Primera, f (7) = 5, de modo que f está definida en x = 7.

Segunda, por tanto, f tiene limite cuando X —> 7

Tercera por tanto f es continua en 7.

Ej. 2: Demostrar que g(x) = x2 — 3 es continua en — 4.

Solución: la función g está definida en x = — 4; g (—4) = 13. También:

Por tanto, g es continua en — 4.

3.9 Tipos de discontinuidad.

Una función g(r) se dice que es continua en r = x, cuando se cumple una de las condiciones siguientes:

1). g(r) debe ser definida en r = x.

2). g(r) debe existir y además ser finita.

3). g(r) debe existir y ser finito.

Si alguna de las condiciones falla, se dice que la función es discontinua en r = x. Si así consta generalmente, una función discontinua es aquella cuya gráfica no se puede dibujar sin levantar la mano / el lápiz. Esto se debe a la existencia de “puntos aislados” en la gráfica de la función.

1). La Discontinuidad Asintótica: Esta variedad de la discontinuidad se produce cuando la función correspondiente no está conectada a la recta asintótica.

2). Discontinuidad en un Punto: Tal tipo de discontinuidad se produce cuando una determinada función se delinea explícitamente para un valor fuera de esta. La Discontinuidad en un punto se produce en un punto particular. Estas discontinuidades son también conocidas como singularidades removibles, o discontinuidades singulares.

3). Discontinuidad de Salto: En caso que la función se mueva hacia dos valores diferentes en cada parte de la discontinuidad, se dice entonces que ocurre la discontinuidad de salto. El nombre de “discontinuidad de salto” viene del hecho de que los valores de una función particular saltan en un punto difícil. Las Discontinuidades de Salto también se conocen con el nombre de Discontinuidad de Primer Tipo o discontinuidad simple. Este tipo de discontinuidad se encuentra generalmente en funciones a trozos. Estas funciones se definen en pedazos.

Ejemplo:

La función g(r) es definida como

g(r) = r2, r ≤ 1 6 – r, r > 1 

Ahora, en r = 1, estas dos definiciones de la función tienen valores diferentes y se puede ver que g(r) salta a la derivación mas próxima en r = 1. Es debido a este salto, que se dice que la función es discontinua.

No todas las funciones muestran discontinuidad de salto. La discontinuidad se basa sólo en las dos piezas de la función.

Bibliografía:

https://darkcity2111.wordpress.com/limites-de-sucesion/

http://mitecnologico.com/igestion/Main/LimiteDeUnaSucesion

http://ocw.unizar.es/ocw/pluginfile.php/72/mod_label/intro/u7funreto.pdf

https://electromecanics2011.wordpress.com/3-2-limite-de-una-funcion-de-variable-real/

http://www.vitutor.com/fun/3/a_5.html

http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites

http://www.fca.unl.edu.ar/Limite/2.2%20L%EDmiteslaterales.htm

https://matedos.wordpress.com/2009/09/13/limites-laterales/

http://www.mat.uson.mx/~jldiaz/limites_al_infinito.html

http://mitecnologico.com/igestion/Main/Asintotas

http://www.vitutor.com/fun/5/t_e.html

http://www.vitutor.com/fun/3/b_5.html

http://mitecnologico.com/igestion/Main/TiposDeDiscontinuidades