Calculo Diferencial

Unidad 1 NÚMEROS REALES

Juan Isaias Cañedo Huerta           15260694

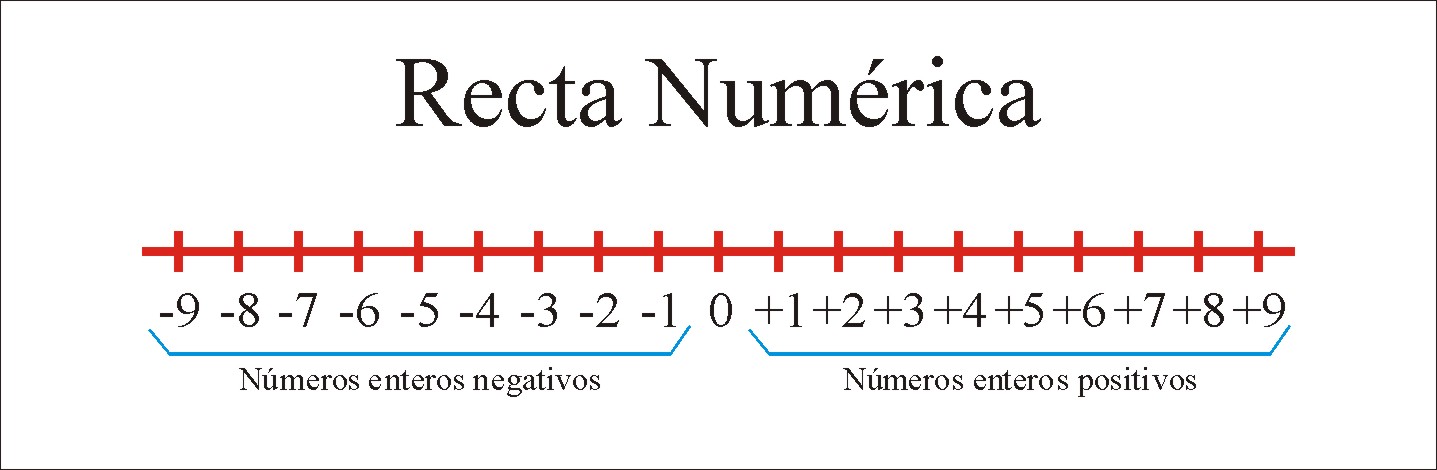
1.1 La recta numérica.

Una recta numérica representada por dos flechas en los extremos, es una recta infinitamente larga y es una parte esencial de las matemáticas básicas.

Los puntos en una recta numérica corresponden a un número real específico.

Todos los puntos están marcados a una distancia específica del origen que es 0, el cual puede ser elegido arbitrariamente.

La recta numérica es una herramienta muy útil para entender los conceptos de números enteros con signo y números reales, así como su suma y resta.

A partir del origen en la recta numérica, los números siguen aumentando en magnitud hacia la derecha, mientras que se mantienen disminuyendo en magnitud en la dirección opuesta, que es representado por el símbolo negativo.

La recta numérica (números reales) consiste de tres clasificaciones de los números reales, las cuales son;

1.- Los números reales negativos: son aquellos que están a la izquierda del origen.

2.- El numero 0 es el punto de origen.

3.- Los números reales positivos: son los que se encuentran a la derecha del origen.

Ejercicios:

Pedro camina tres pasos hacia la derecha y luego cinco en la misma dirección ¿a cuántos pasos se encuentra de la posición inicial?.

Angie se desplaza 4 m. hacia la derecha y luego 7 m. hacia la izquierda. ¿A qué distancia se encuentra del punto de partida?

Edward se desplaza 3 m. hacia la izquierda y 5 m.  más hacia la izquierda. ¿A que distancia se encuentra del punto de partida?.



Representa la operación en la recta numérica.

A)  – 7  +  (– 2 ) = -9




B) – 4 +  13 = 9


 C) – 3 + (– 1 ) + 8 = 4


D) – 4 + (– 1) + (– 3) + 9 = 

1.2 Los números reales.

Los números reales son parte primordial de las matemáticas, ya que son todos los números que pueden ser representados en una recta numérica.

Los números reales comprenden:

• Los números positivos.

• Los números negativos.

• El cero.

• Las fracciones.

• Los decimales.

• Los números racionales.

• Los números irracionales.

Generalmente el conjunto de los números reales es representado por la letra “R”, y se les aplican las operaciones y las diferentes propiedades de operación estudiadas en aritmética y en álgebra.

 Se puede definir a los números reales como el conjunto de todos los números con que realizamos operaciones matemáticas habitualmente en aritmética y álgebra.

Ejemplo de números reales:

• Números naturales: {12345678910…}
• Números enteros positivos = {1, 2. 3, 4, 5, 6,7, 8, 9}
• Números enteros negativos = { -1, -2, -3, -4, -5, -6, -7, -8, -9}
• Cero: 0
• Números fraccionarios: ½, ¼, 14/35, 2/7
• Números decimales: .25 0.999, 0.625
• Números racionales: .125 y 1/8, .5 y ½, .85 y 17/20
• Números irracionales: p = 3.14159265358979323846… (pi); j  = 1.618033988749894848204586834365638117720309… (phi, Número Aureo); √1

Ejercicios:

1.3 Propiedades de los números reales.

Las propiedades que existen en los números reales son indispensables tanto por la ordenación de los numero,como también para poder hacer soluciones a los problemas matemáticos que se nos pueda dificultar. Así también los podemos observar y comprender mejor, como obtener soluciones y como es su representación.

En estas tenemos los axiomas las cuales son las siguientes:

• Asociadas suma:   (a+b)+c = a+(b+c)
• Conmutativa suma: a+b=b+a
• Conmutativa multiplicación: a*b= b*a
• Asociativa multiplicación: a(bc)=(a*b)=c
• Distributiva a(b+c)=ab+ac
• Elemento neutro aditivo: a+0=a
• Elemento neutro multiplicativo: a*1=a
• Elemento inverso aditivo: a+(-a)=a
• Elemento inverso multiplicativo: a*a-1= 1 o (a* 1/a 1)

La siguiente tabla resume las propiedades de los números reales:

Ejercicios:

Indique qué propiedad de los números reales se ilustra con cada ejemplo.

A) –3 + 3 = 0.                       Respuesta: elemento inverso para la suma.

B) (x + y) × z = xz + yz.       Respuesta: ley distributiva.

C) (–3)(6) = (6)(–3).             Respuesta: ley conmutativa para el producto.


Elige la propiedad de las operaciones con números reales que aplica en cada caso:

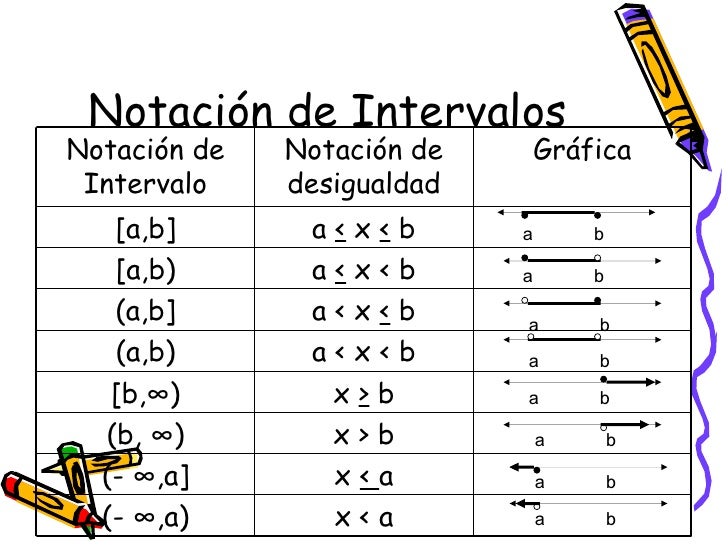
1.4 Intervalo y su representación mediante desigualdades.

Un intervalo es un segmento de la recta numérica comprendido entre dos valores extremos a y b.

Una desigualdad es de una forma: 10 + 3 es mayor que 6.

Se le representa por: Desigualdad: 10 + 3 > 6

Esta desigualdad se transforma en inecuación, cuando se introduce una incógnita: Inecuacion: 10 + x > 6

Tipos de intervalo

Intervalos cerrados
Son aquellos intervalos que incluyen los valores extremos a y b. Esto se expresa con la desigualdad   a ≤ x ≤ b, que significa que a es menor o igual que x y que x es menor o igual que b.
Otra manera de expresar intervalos cerrados es utilizando corchetes: [a , b].

Intervalos abiertos
Son aquellos intervalos que excluyen los valores extremos a y b. Esto se expresa con la desigualdad  a < x < b, que significa que a es menor que x y que x es menor que b.
Otra manera de expresar intervalos abiertos es utilizando paréntesis: (a , b).

Intervalos semi-abiertos
Son aquellos intervalos que solo incluyen a uno de sus extremos.
Existen dos casos:

Abiertos por la izquierda

Se representan con la desigualdad  a < x ≤ ∞, que significa que a es menor que x y que x es menor o igual que b.

También se puede expresar así: (a , b].

Abiertos por la derecha 

Se representan con la desigualdad  a ≤ x < b, que significa que a es menor menor o igual que x y que x es menor que b.
También se puede expresar así: [a , b).

Infinitos por la izquierda

Existen dos casos:
Contiene al extremo b. (-∞ , b].
Se representan con la desigualdad  -∞ < x ≤ b

No contiene al extremo b. (-∞,b).
Se representan con la desigualdad  -∞ < x < b

Infinitos por la derecha

Existen dos casos:
Contiene al extremo a. [a,∞)
Se representan con la desigualdad a ≤ x < ∞

No contiene al extremo a. (a,∞)
Se representan con la desigualdad a < x < ∞

Ejercicios:

Representa mediante desigualdades los siguientes intervalos.

1)  [-3 , 5].        Respuesta: -3 ≤ x ≤ 5.  

2) (4 , 19).        Respuesta: 4 < x < 19.    

3) (0 , 6.5].       Respuesta: 0 < x ≤ 6.5.       

4)  [-1 , -1/3).    Respuesta: -1 ≤ x < -1/3.     

5)  (-∞ , -7/2).   Respuesta: -∞ < x < -7/2.  

6) (-∞ , 2].        Respuesta: -∞ < x ≤ 2 .    

7)  [-1 , ∞).       Respuesta: -1 ≤ x < ∞.

1.5 Resolución de desigualdades de primer grado con una incógnita y de desigualdades.

Las desigualdades de primer grado (lineales), se puede resolver de una manera similar a las ecuaciones lineales. Es decir, se puede despejar la incógnita utilizando operaciones idénticas en ambos lados.

Es necesario tomar en cuenta una diferencia muy importante, pues cuando se multiplica una desigualdad por algún valor negativo, la dirección de la desigualdad se invierte, es decir "de menor" que cambia a "mayor que" y viceversa.

Desigualdades de segundo grado con una incógnita

De acuerdo a las características de la expresión cuadrática, podemos determinar si la resolveremos por fórmula general, por factorización, ó despejando.
Además de tener en cuenta el efecto de la multiplicación por números negativos en la dirección de la desigualdad, también tenemos que considerar el efecto de la raiz cuadrada. Este efecto lo explicaremos en los ejemplos.
El resultado lo representaremos en notación de intervalos y con representación sobre la recta numérica

.Ejemplos

Resolveremos un de ejemplo de desigualdad.

A) Aquí tenemos una de primer grado con una incógnita.

1) 3x – 5 ≥ 5x + 15

Sumamos 5 a los dos lados de la desigualdad
3x – 5 + 5 ≥ 5x + 15 + 5
3x ≥ 5x + 20

B) Ahora resolveremos desigualdades de cuadráticas con una incógnita.

3) x2 > 3x + 4

Primero expresamos la desigualdad como una ecuación y resolvemos.
x2 = 3x + 4

Restamos (3x + 4) a los dos lados para que uno de los lados quede con valor cero.
x2 – (3x + 4) = 3x + 4 – (3x + 4)
x2 – 3x – 4 = 0

Ejercicios.

Resuelve las siguientes desigualdades:

1)

 (1/3)x + 1/2 < -2x + 1

(1/3)x + 1/2 – 1/2 < -2x + 1 – 1/2
(1/3)x < -2x + 1/2

(1/3)x + 2x < -2x + 1/2 + 2x
(7/3)x < 1/2

3/7(7/3)x < 3/7(1/2)
x < 3/14

Respuesta: (-∞ , 3/14)

2) 

4) -4x2 + x + 5 ≥ 0

x1 = -1 y x2 = 5/4

(-∞ , -1]

-4(-3)2 + (-3) + 5 ≥ 0
-34 ≥ 0 FALSO

[-1 , 5/4]
-4(1)2 + 1 + 5 ≥ 0
2 ≥ 0 VERDADERO

[5/4 , ∞)
-4(2)2 + 2 + 5 ≥ 0
-9 ≥ 0 FALSO

Respuesta: [-1 , 5/4]

3) 

4)

5)

6)

7)

1.6 Valor absoluto y sus propiedades.

El valor absoluto de cualquier número es siempre positivo. Este valor puede ser conocido también como el módulo del número.

El valor absoluto de un número x se escribe como | x |, y se lee como “módulo de x”.

Por ejemplo, la posición de 2 y −2 en la recta numérica indica que −2 <2, pero que ambos están a la misma distancia de 0.

Por lo tanto, se dice que −2 y 2 tienen el mismo valor absoluto.

Las propiedades fundamentales del valor absoluto son:

1º Propiedad multiplicativa

Nos dice que “El valor absoluto de un producto es igual a el producto de los valores absolutos

2º Preservación de la división (equivalente a la propiedad multiplicativa)

Nos dice que “El valor absoluto de un cociente es igual a el cociente de los valores absolutos solo si el denominador no es cero”

3º Propiedad de la simetría

Nos dice que “El valor absoluto del opuesto de un numero es igual a el valor absoluto del numero”

4º Definición positiva

Nos dice que “El único numero que su valor es 0 es el mismo 0”

5º No negatividad

Nos dice que “El valor absoluto de cualquier numero nunca va a dar negativo”

6º Identidad de Indescernibles

Nos dice que “Cuando el valor absoluto de una adición de dos números es 0 entonces o bien y son el mismo numero o son opuestos uno del otro”.

7º Propiedad aditiva

Nos dice que “El valor absoluto de una suma de dos numero es menor o igual a la sumas de los valores absolutos”.

8º Equivalente a la propiedad aditiva

Nos dice que “El valor absoluto de una resta de dos números es mayor o igual a el valor absoluto de la resta de los valores absolutos”.

9º Desigualdad triangular.


Ejercicios:

Elige la opción correcta:

1)

 2)

 3)

 4)

 5)

 6)

7)

1.7 Resolución de desigualdades que incluyan valor absoluto.

La solución de desigualdades que implican valor absoluto requiere algunos conceptos básicos. La definición básica “ El valor absoluto de un número es siempre positivo” no tiene ningún uso mientras se resuelven tales desigualdades.

En la resolución de este tipo de desigualdades aplicaremos en primera instancia una de las cuatro últimas fórmulas, dependiendo del caso.

1) Mayor o igual que ≥

2) Mayor que >

3) Menor o igual que ≤

4) Menor que <

Por ejemplo: | x + 3 | <7

De acuerdo con el patrón, puede ser re-formulada como

 = - 7 <x + 3 <+7

Después de replanteada siguiendo el patrón 1, ahora puede ser resuelta de acuerdo con los fundamentos de la desigualdad, es decir,

  - 7 – 3 < x < + 7 – 3

  - 10 < x < +4

Por tanto, la solución está en el intervalo de (−10, +4).

Ejercicios.

Resuelve las siguientes desigualdades con valor absoluto.

1) 

2) 

3) 

(-15, 5)

 4)

(-∞, -4) U (8, ∞)

5)

(-8,8)

6)

7)

Bibliografía:

http://calculodiferencial-ax.blogspot.mx/2012/08/11-la-recta-numerica.html

http://www.ejemplode.com/5-matematicas/2419-ejemplo_de_numeros_reales.html

https://celsomates.files.wordpress.com/2009/09/nc3bamero_real_sol.pdf

https://sites.google.com/site/mago9292/unidad-1-numeros-reales/1-3---propiedades-de-los-numeros-reales

http://www.vitutor.com/di/re/r3e.html

https://asesoriasmfq.wordpress.com/cursos/calculo-diferencial/u1-numeros-reales/1-4-intervalos-y-su-representacion-mediante-desigualdades/

https://asesoriasmfq.wordpress.com/cursos/calculo-diferencial/u1-numeros-reales/1-5-resolucion-de-desigualdades-de-primer-grado-con-una-incognita-y-de-desigualdades-cuadraticas-con-una-incognita/

http://mitecnologico.com/igestion/Main/ValorAbsolutoYSusPropiedades

http://matematicasyfunciones.blogspot.mx/2012/03/valor-absoluto-y-sus-propiedades.html

http://mitecnologico.com/igestion/Main/ResolucionDeDesigualdadesQueIncluyanValorAbsoluto

http://www.virtual.unal.edu.co/cursos/sedes/fundamentacion/uv00009/lecciones_html/cap2/algebra14.html

http://es.slideshare.net/sitayanis/5-inecuaciones-con-valor-absoluto-9384355?next_slideshow=1