Unidad 4: Derivadas.
Cañedo Huerta Juan Isaias No. control: 15260694
4.1 Conceptos de incremento y razón de cambio. La derivada de una función.
La derivada de una función es un vector que apunta hacia la dirección donde la función ve un mayor incremento en su valor.
A la luz de la afirmación anterior se puede concluir que la derivada de la función es generalmente cero en algunos mínimos locales o máximos locales dado que en esa posición la función no nota incrementos hacia una dirección en particular.
La pendiente de una línea recta se puede calcular como:
La expresión anterior se denomina como cociente de la diferencia. Esto se debe a que representa la diferencia entre dos cocientes.
La tasa o razón de cambio puede ser constante o no. Una tasa de cambio constante es aquella que no cambia durante un período de tiempo.
Como sabemos la variación en la tasa es un cociente de la diferencia, la tasa instantánea de cambio será el límite de esos cocientes.
La tasa de cambio instantánea es popularmente conocida por el nombre de derivada.
No es posible calcular la derivada de una función en algún instante determinado, por tanto la derivada de una función se calcula sobre un intervalo, aunque este intervalo sea muy pequeño.
Entonces el cálculo de la derivada de una función también se puede hacer mediante el cálculo de la tasa promedio de cambio en intervalos más cortos.
La derivada de cualquier función, no solamente una función del tiempo, puede interpretarse como una razón de cambio instantánea con respecto de la variable independiente. Si y=f(x), entonces la razón de cambio promedio de y (por un cambio unitario en x) en el intervalo [x,x+"x] es el cociente.
Ejemplo:
Determinar el valor exacto de la derivada, tome el límite de la función como h. Por lo cual la derivada de la función se calcula como; Lim f(x + h) – f(x)/ h h → 0.
4.2 La interpretación geométrica de la derivada.
Además de evaluar el valor de una función en cierto punto, también es esencial que evaluemos la variación en el valor de la función a medida que la entrada de la función varía.
Esto se conoce como la pendiente de la recta en el caso de una recta lineal. Mientras que para una recta curva, la pendiente de la recta varía en cada punto. Esto significa que para una línea recta / función lineal se obtiene un número constante como su pendiente. Mientras que para una recta curva la pendiente es una función del valor de entrada de la función.
La noción de derivada puede explicarse de dos maneras, una como la pendiente de la curva, que es la representación geométrica, y la otra como la tasa de variación, que es la representación física. La pendiente de la tangente de la curva extrae la derivada de la función geométrica.
Supongamos que una función f(x) = x2. La gráfica de la función luciría de la siguiente forma:
La curva de color azul representa el gráfico de la función. Tome dos puntos en el eje x, supongamos x y x0 como en el gráfico de arriba.
Determine el valor de la función en esos valores de x. Ahora trace una línea que pase por esos puntos sobre la curva de la función para obtener una línea recta. La línea roja en el gráfico anterior representa esa línea.
A medida que muevo los puntos sobre el eje x más cerca uno del otro conseguimos una recta menos pronunciada que pasa a través de la curva de la función. En el instante que
x = x0, la gráfica se vería así;
Ejemplo:
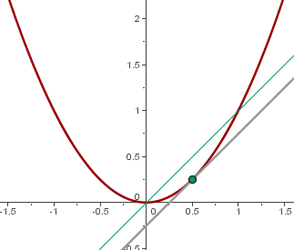
Dada f(x) = x2, calcular los puntos en los que la recta tangente es paralela a la bisectriz del primer cuadrante.
La ecuación de la bisectriz del primer cuadrante es y = x, por tanto su pendiente es m= 1.
Como las dos rectas son paralelas tendrán la misma pendiente, así que:
f'(a) = 1.
Dado que la pendiente de la tangente a la curva es igual a la derivada en el punto x = a.
4.3 Concepto de diferencia, interpretación geométrica de los diferenciales.
Existen muchas situaciones, dentro y fuera de las matemáticas, en que necesitamos estimar una diferencia, como por ejemplo en las aproximaciones de valores de funciones, en el cálculo de errores al efectuar mediciones (Valor real menos valor aproximado) o simplemente al calcular variaciones de la variable dependiente cuando la variable independiente varía "un poco", etc. Utilizando a la recta tangente como la mejor aproximación lineal a la función en las cercanías del punto de tangencia, aproximaremos esta DIFERENCIA con la diferencia sobre la recta tangente, a la que llamaremos EL DIFERENCIAL de la función en el punto.
El diferencial está definido en los tratamientos modernos del cálculo diferencial de la siguiente manera.1 El diferencial de una funciónƒ(x) de una única variable real x es la función df de dos variables reales e independientes x y Δx dada por:
Uno, o los dos, argumentos pueden ser suprimidos:
ej., se puede ver df(x) o simplemente df. Si y = ƒ(x), el diferencial también puede ser escrito dy. Dado que dx(x, Δx) = Δx es convencional escribir dx = Δx, de manera que la igualdad se mantiene.
Interpretación geométrica del diferencial.
Interpretación geométrica del diferencial de una función en un punto.
El diferencial se puede tomar en el sentido geométrico como la elevación de la tangente desde el punto en que se toma el diferencial.
Recuérdese que la derivada de la función en el punto es la pendiente de la recta tangente a la función en el punto, como sabemos que la tangente de un ángulo es igual al cociente entre el cateto opuesto (incremento de y) y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, sólo hay que despejar el incremento de y que equivale a nuestro diferencial.
Vista geométricamente, la elevación se produce verticalmente a partir del punto en que se toma el diferencial. El incremento que se tome representará el alejamiento horizontal que haga desde el punto en cuestión.
Así la elevación de la tangente que se obtenga como resultado dependerá del punto en cuestión y del alejamiento horizontal que se tomen, que en la formulas matemáticas están definidos respectivamente por y .
Ejemplo: Verifique que;
a) Para f(x) = x2 se cumple que D f @ df en xo = 1 y h = 0.1
Solución:
D f = f(1.1) - f(1) = 1.21 - 1 = 0.21
df = f ' (1)dx =(2x|x=1 )(0.1) = (2)(0.1) = 0.20
La variación real difiere de la aproximada en una centésima.
b) Para f(x) = x2 se cumple que D f @ df en xo = 1 y h = -0.1
Solución:
D f = f(0.9) - f(1) = 0.81 - 1 = -0.19
df = f ' (1)dx =(2x|x=1 )(-0.1) = (2)(-0.1) = -0.20
La variación real difiere de la aproximada en una centésima..
c) Para f(x) = x2 se cumple que D f @ df en xo = 2 y h = 0.006
Solución:
D f = f(2.006) - f(2) = 4.024036 - 4 = 0.02403
df = f ' (2)dx =(2x|x=2 )(0.006) = (4)(0.006) = 0.02400
La variación real difiere de la aproximada en tres cienmilésimas.
4.4 Propiedades de la derivada.
Las derivadas forman una parte importante del cálculo.
Hablando en términos sencillos, la derivada es una medida de la tasa de variación de la salida de una función así como varía la entrada de la función.
En base a la definición anterior está claro que la salida de la función es una función de la entrada de la función.
Las derivadas tienen algunas propiedades especiales que son importantes estudiar antes de saltar de lleno en el tema.
Algunas de las propiedades más importantes son las siguientes:
1. Si la función f(x): X → Y es diferenciable en un punto P, entonces se puede concluir que la función f(x) es continua en el punto p.
2. La derivada de la suma de dos funciones es igual a la suma de las derivadas de las dos funciones tomadas individualmente. La misma regla aplica también para la resta de dos derivadas. Esta regla es más conocida por el nombre de la regla de la linealidad.
3. La derivada de la multiplicación de una cantidad escalar con una función es igual a cuando la cantidad escalar se multiplica a la derivada de la misma función.
4. La derivada de un número constante es siempre igual a cero.
5. La diferenciación de una variable con respecto a si misma producirá uno.
6. La derivada de la multiplicación de dos funciones es lo mismo que sumar la multiplicación de la primera función con la derivada de la segunda función y la multiplicación de la segunda función con la derivada de la primera función. Esta regla se conoce más comúnmente con el nombre de la regla del producto.
7. La derivada de una variable elevada a una potencia es igual a las veces de la potencia de la derivada de la misma variable elevada a una potencia reducida por uno. Esta regla es mejor conocida por el nombre de la regla de la potencia. Es esencial que n sea un número real para que la propiedad anterior sea cierta.
8. La derivada de la división de una función con alguna otra función es lo mismo que la división de la resta de la multiplicación de la primera función con la derivada de la segunda función y la multiplicación de la segunda función con la derivada de la primera función con el cuadrado de la segunda función. Aquí el valor de la función no debería ser igual a cero. Esta regla se conoce por el nombre de la regla del cociente.
Ejemplo:
Resuelva las siguientes derivadas según la propiedad que le corresponda:
4.5 Regla de la cadena
Una función compuesta es una función que implica la imposición de una función a otra función. Sea f(x) una función que es diferenciable sea g(x) cualquier otra función que también es diferenciable. Entonces, al imponer f(x) a g(x) se produce una nueva función h(x), la cual es una combinación de las dos funciones diferenciables. h(x) = f(x) 0 g(x) Considere una función, para la cual debe encontrar la derivada, y(x) = (x2 + 4x +5) Sería bastante fácil de encontrar.
Pero si fuese encontrar la derivada de una función como la siguiente, y(x) = (x3 + 4x +5)60 entonces sería un problema, a pesar de que sus derivadas pueden ser despejadas, pero si existiera una regla que hiciera el problema fácil de resolver entonces habría sido mucho más simple.
Para resolver este problema de encontrar las derivadas de una función compuesta, Leibniz introdujo la regla de la cadena, que tenía la intención de encontrar la derivada de funciones compuestas.
De acuerdo con la regla de la cadena, las derivadas pueden ser consideradas como fracciones a fin de resolver el problema como;
Así que la regla de la cadena para la diferenciación de una función compuesta es la siguiente;
Ejemplos.
4.6 Formulas de derivación y formulas de diferenciación.
Para funciones más simples, el trabajo de calcular la derivada de una función se puede realizar simplemente usando la definición de derivada. Pero si se da una función compleja, ahora es que vale la pena utilizar la definición de la derivada para el cálculo de las derivadas de la función, dado que si no lo hacemos requeriría muchos cálculos.
Con el fin de reducir los cálculos involucrados en el proceso se han introducido una serie de fórmulas de diferenciación. Junto con las fórmulas se han introducido una serie de propiedades que pueden ser usadas directamente. Algunas fórmulas de diferenciación importantes son;
1.- Fórmula de Diferenciación General.
 en esta fórmula, c es un valor constante
en esta fórmula, c es un valor constante esta es la regla de la potencia de la diferenciación. En esta fórmula, n debe ser exclusivamente un número real.
esta es la regla de la potencia de la diferenciación. En esta fórmula, n debe ser exclusivamente un número real. Lo que significa que cuando un número es diferenciado con respecto a sí mismo producirá uno como resultado.
Lo que significa que cuando un número es diferenciado con respecto a sí mismo producirá uno como resultado.2.- Fórmulas de Diferenciación; Funciones Logarítmicas.
 Lo que significa que la diferenciación del logaritmo natural de un número con el mismo número producirá la inversa del número como resultado.
Lo que significa que la diferenciación del logaritmo natural de un número con el mismo número producirá la inversa del número como resultado. Esta ecuación explica que la diferenciación de un logaritmo natural de la función con respecto a la variable de entrada producirá el inverso de la multiplicación de la función con la derivada de la función como salida.
Esta ecuación explica que la diferenciación de un logaritmo natural de la función con respecto a la variable de entrada producirá el inverso de la multiplicación de la función con la derivada de la función como salida.3.- Fórmulas de Diferenciación; Funciones Exponenciales.
Esta fórmula de diferenciación es interesante dado que establece; la diferenciación del exponente de una variable producirá el exponente de la variable como salida.

Esta regla establece que la diferenciación del exponente de una función producirá la multiplicación del exponente de la función con la derivada de la función como salida.
Esta regla establece que la diferenciación de una constante elevada a la potencia de una variable producirá la multiplicación de la constante elevada a la potencia de la misma variable con el logaritmo natural de la constante.
A continuación se muestra una imagen con las formulas de derivación:
Ejemplos resueltos:
Calcula mediante la fórmula de la derivada de una raíz:
Deriva las siguientes funciones exponenciales:
4.7 Derivadas de orden superior, regla de L'Hopital.
La Regla de L’Hopital establece que bajo ciertas condiciones, el límite del cociente de dos funciones f(x)/g(x) coincide con el límite del cociente de sus derivadas.
La derivada de cualquier función determina la tasa de variación en función de la función con respecto a la entrada de la función. Este proceso de encontrar la derivada de una función se puede aplicar en una cascada muchas veces para encontrar las derivadas de orden superior de la función.
En términos simples diferenciar la derivada de una función dará lugar a una derivada de la función de orden superior por un grado. La derivada de primer orden de la función se representa como;
La derivada de primer orden de la función se representa como:

La derivada de segundo orden de una función se representa como:

La derivada de tercer orden de una función se representa como:

Y así sucesivamente. La derivada de segundo orden de la función también se conoce como “g doble prima de y”, donde g es la función en términos de y. De manera similar la derivada de tercer orden de una función también se conoce como “g triple prima de y”, etc. Las derivadas de orden superior de cualquier función pueden derivarse de esta forma hasta que la derivada obtenida es diferenciable en sí misma.
NOTA: No es posible obtener una derivada de orden superior de la función si la derivada actual de la función no es diferenciable.
La regla de L’Hôspital, también llamada regla de Bernoulli es una parte muy importante del cálculo. Se utiliza principalmente para encontrar las salidas de los límites cuando los límites son de forma intermedia; se utiliza principalmente para las derivadas de las funciones. Esta regla se utiliza para transformar los límites intermedios en una forma determinada y por tanto, obtener la salida más conveniente.
La regla de L´Hôpital permite resolver muchos casos de indeterminación de límites de funciones en un punto x = a.
Ejemplos:
4.8 Derivadas de funciones implícitas.
Las funciones se pueden clasificar en dos categorías generales, funciones implícitas y funciones explícitas.
Una función se denomina implícita cuando su salida no está definida en términos de su entrada, explícitamente.
Las funciones algebraicas y las funciones inversas corresponden a la categoría de funciones implícitas.
Una función que se define implícitamente puede ser diferenciada con la ayuda de una regla de la cadena, denominada diferenciación implícita. La mejor forma de diferenciar una función implícita es diferenciando cada lado de la ecuación de la función explícitamente.
Mientras se hace esto, es esencial tener en mente que la variable dependiente de la función debe ser tratada como la variable independiente de la función; y sencillamente aplicar las reglas de diferenciación normal incluyendo todas las propiedades y las reglas de diferenciación.
Los pasos para la diferenciación de una función implícita se indican a continuación:
1. Diferencie la ecuación implícita con respecto a x tal como lo hace para una función explícita. Si la ecuación contiene términos de y o cualquier otra variable elevada a la potencia de y, entonces primero multiplique la ecuación con dy / dx.
2. Mueva los términos con dy / dx como sus coeficientes a un lado de la ecuación y el resto de los términos hacia el otro lado de la ecuación.
3. Ahora, extraiga el valor de dy / dx y resolverlo.
Hay una forma más de resolver una función implícita, llamada diferenciación directa.
Bajo el método explicado anteriormente, el primer paso es escoger la variable que se considerará como variable dependiente y la variable que se considerará como variable independiente.
Suponga que y es la variable dependiente para la función dada, luego se resuelve para y con respecto a x, que es la variable independiente de la función.
Bajo el método de diferenciación directa, sólo resuelva para la variable dependiente al mover los términos contenidos en la variable dependiente hacia un lado y la variable independiente hacia el otro lado y realizando la diferenciación con respecto a la variable independiente.
Bajo el método de diferenciación directa, generalmente la variable dependiente se da de manera explícita y no de forma escogida.
Ejemplo: Derivar las siguientes funciones:
Bibliografía:
http://mitecnologico.com/igestion/Main/ConceptosDeIncrementoYDeRazonDeCambioLaDerivadaDeUnaFuncion
http://mitecnologico.com/igestion/Main/InterpretacionGeometricaDeLaDerivada
http://www.mat.uson.mx/eduardo/calculo2/soldifer/soldiferHTML/diferencial.htm
http://mitecnologico.com/igestion/Main/PropiedadesDeLaDerivada
http://www.vitutor.com/fun/4/d_e.html
http://mitecnologico.com/igestion/Main/ReglaDeLaCadena
http://www.vitutor.com/fun/4/b_7.html
http://mitecnologico.com/igestion/Main/FormulasDeDerivacionYFormulasDeDiferenciacion
http://www.vitutor.com/fun/4/b_a.html
http://www.ehu.eus/juancarlos.gorostizaga/apoyo/lim_lhopital.htm
http://www.unizar.es/aragon_tres/unidad7/u7der/u7derte40.pdf
http://mitecnologico.com/igestion/Main/DerivadaDeFuncionesImplicitas
http://www.vitutor.com/fun/4/b_11.html




















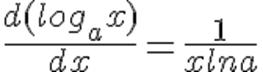






















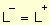

 si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.
si para los valores de x proximos a a, x→ a los valores de f(x) pueden hacerse tan grandes como queramos.



